Trigonometry formulas are crucial for SSC CGL exams because they are extensively used in solving geometry, mensuration, and algebraic problems. These formulas help candidates solve questions related to angles, distances, heights, and velocities, which are commonly asked in SSC CGL exams. Mastering trigonometry formulas enables candidates to efficiently tackle questions from various sections like quantitative aptitude and reasoning, thereby improving their overall performance in the exam.

Table of Contents
Introduction to Trigonometry
Trigonometry is a branch of mathematics that deals with the study of relationships between angles and sides of triangles. It has various applications in fields such as engineering, physics, navigation and more. In the SSC CGL exam, trigonometry questions often involve solving triangles, finding angles and length of sides, and understanding trigonometric identities.
Trigonometry Formulas
Trigonometry formulas are mathematical expressions that describe relationships between the angles and sides of triangles. These formulas enable us to solve problems involving triangles and angles. They include basic relationships like the Pythagorean theorem, which relates the lengths of the sides of a right triangle, as well as trigonometric ratios such as sine, cosine, and tangent, which express the ratios of the lengths of the sides of a right triangle in terms of its angles.
Trigonometry Formulas for SSC CGL 2024
Basic Trigonometric Ratios
1. Sine (sin): The sine of an angle in a right triangle is the ratio of the length of the side opposite the angle to the length of the hypotenuse.
Sin (θ) = Opposite side/Hypotenuse
2. Cosine (cos): The cosine of an angle is a right triangle is the ratio of the length of the adjacent side to the length of the hypotenuse.
Cosine (θ) = Adjacent side/Hypotenuse
3. Tangent (tan): The tangent of an angle in a right triangle is the ratio of the length of the side opposite the angle to the length of the adjacent side.
Tan (θ) = Opposite side /Adjacent side
4. Cotangent (cot): The cotangent of an angle in a right triangle is the reciprocal of the tangent ratio.
Cot (θ) = Adjacent side/Opposite side
5. Secant (sec): The secant of an angle in a right triangle is the reciprocal of the cosine ratio.
Sec (θ) = Hypotenuse/Adjacent side
6. Cosecant (cosec): The cosecant of an angle in a right triangle is the reciprocal of the sine ratio.
Cosec (θ) = Hypotenuse/Opposite side
Reciprocal Identities
The reciprocal of the fundamental trigonometric ratios sine, cosine, tangent, cotangent, secant and cosecant are:
- Sinθ = 1/Cosecθ or Cosecθ = 1/Sinθ
- Cosθ = 1/Secθ or Secθ = 1/Cosθ
- Tanθ = 1/Cotθ or Cotθ = 1/Tanθ
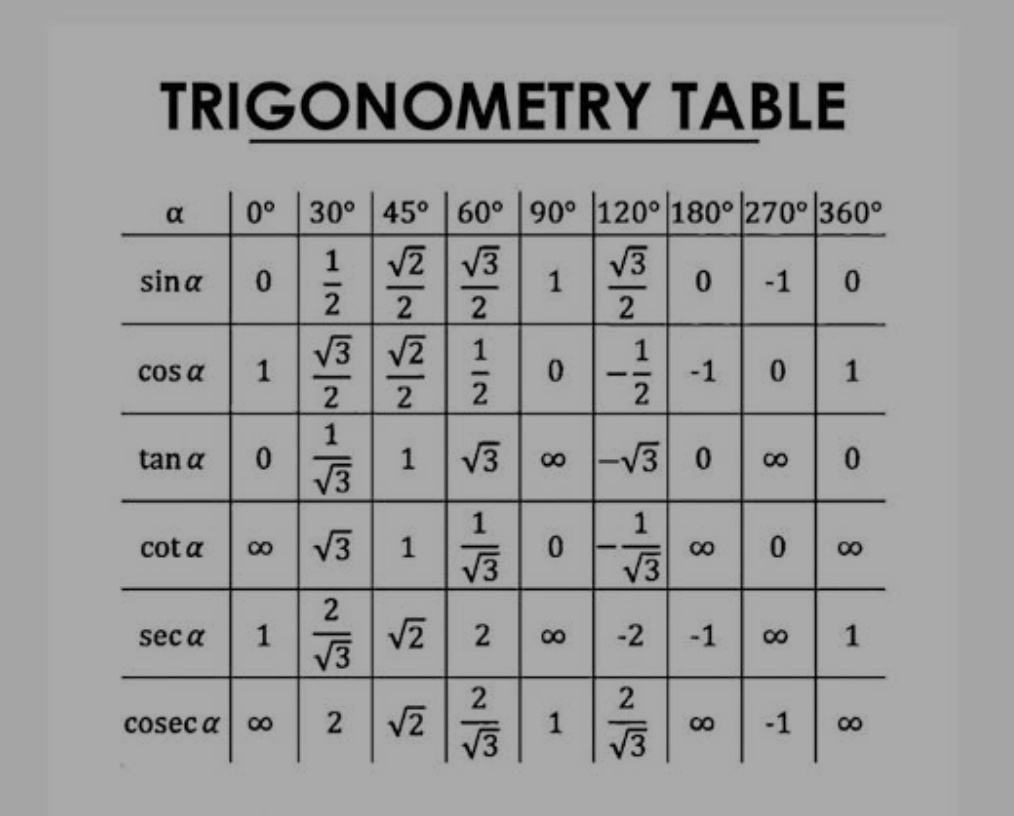
Trigonometry Table
Trigonometric table is essentially a tabular compilation of trigonometric ratio values for various conventional angles such as 0°, 30°, 45°, 60°, and 90° and sometimes unusual angles such as 180°, 270°, and 360°.
Pythagorean Identities
The three main Pythagorean identities are:
- Sin²θ + cos²θ =1
- Tan²θ + 1 = sec²θ
- Cot²θ + 1 = cosec²θ
Pythagorean Theorem
In a right triangle, the square of the length of the hypotenuse (H) is equal to the sum of the squares of the lengths of the other two sides (B and P). i. e H² = P² + B²
Co-function Formulas
The six main co-function identities are:
l. cos θ = sin(90° – θ)
ll. sin θ = cos(90° – θ)
lll. Tan θ = cot(90° – θ )
lV. Cot θ = tan(90° – θ)
V. Sec θ = cosec(90² – θ)
Vl. Cosec θ = sec(90° – θ)
Double Angle Formulas
- Sin2A = 2sinA cosA
- Cos2A = 2cos²A – 1
- Tan2A = 2tanA/1 – tan²A
Triple Angle Formulas
- Sin3A = 3 sinA – 4 sin³A
- Cos3A = 4 cos³A – 3 cosA
- Tan3A = (3 tanA – tan³A) / (1 – 3 tan²A)
Opposite Angle Formulas
- Sin (-A) = -sinA
- Cos (-A)= cosA
- Tan(-A) = -tanA
- Cot(-A) = -cotA
- Sec(-A) = secA
- Cosec(-A) = -cosecA
Angle Addition Formulas
- Sin (A + B) = sinA cosB + cosA sinB
- Sin (A – B) = sinA cosB – cosA sinB
- Cos (A + B) = cosA cosB – sinA sinB
- Cos (A – B) = cosA cosB + sinA sinB
- Tan (A + B) = (tanA + tanB)/(1- tanA tanB)
- Tan (A – B) = (tanA – tanB)/ (1+tanA tanB)
Product-to-Sum Formulas
- SinA sinB = ½ [cos(A-B) – cos(A+B)]
- CosA cosB = ½ [ cos(A-B) + cos(A+B)]
- SinA cosB = ½ [ sin(A+B) + sin(A-B)]
- CosA sinB = ½ [ sin(A+B)- sin(A-B)]
Sum-to-Product Formulas
- SinA + sinB = 2 sin [(A+B)/2].cos[(A-B)/2]
- SinA – sinB = 2 sin [(A-B)/2]. cos [(A+B)/2]
- CosA + cosB = 2 cos[(A+B)/2. cos[(A-B)/2]
- CosA – cosB = -2sin [(A+B)/2. sin [(A-B)/2]]
Law of Sines
The Law of Sines defines the ratio of sides of a triangle and their respective sine angles are equivalent to each other.
a/(sin A) = b/(sin B) = c/(sin C)
Law of Cosines
The Law of Cosine states that for any given triangle say ABC; with sides a, b, c, , we have:
- a² = b² + c² – 2bc cosA
- b² = a² + c² – 2ac cosB
- c² = a² + b² – 2ab cosC
Practice Questions
Q1 If tan4θ = cot (40° – 2θ), then θ is equal to:
Solution: Given, tan4θ = cot(40° – 2θ)
= If tanA = CotB
= Then A + b = 90°
= Therefore, 4θ + 40° – 2θ = 90°
= 2θ = 90° – 40° = 50°
= θ = 50°/2
= θ = 25°
Q2 If A + B = 45°, then the value of 2(1 +tanA)(1 + tanB) is:
Solution: If we Put, A = 45°, and B = 0°
= Then, 2(1 + tanA) (1 + tanB)
= 2 (1 + 1) (1 + 0) = 4`
Q3 Cosec (85° + θ) – sec(5° – θ)-tan (55° + θ)+cot(35°- θ) = ?
Solution: Cosec (85° + θ) – sec (5° – θ) – tan (55°+θ) + cot (35° – θ)
= Cosec (85° + θ) – sec (90° – 5° + θ) – tan (55° + θ) + cot (90° – 35° + θ)
= Cosec (85° + θ) – cosec (85° + θ) – tan(55° + θ) + tan (55° + θ)
=0
Q4 Sin²42° + sin²48° + tan ²60° – cosec 30° = ?
Solution: Sin²42° + sin²48° + tan²60° – cosec30° [sin²48° = cos²48°]
= cos²48° + sin²48° + tan²60° – cosec30° [sin²θ + cos²θ=1]
= 1 + 3 – 2
= 2
Q5 If (cos²θ – 1) (1 + tan²θ) + 2tan²θ = 1, (0°≤ θ ≤90°), then θ is:
Solution: (cos²θ – 1) (1 + tan²θ) + 2tan²θ= 1
= -sin²θ.sec²θ + 2tan²θ = 1
= -tan²θ + 2tan²θ = 1
= tan²θ =1
= tanθ = √1
= tanθ = 1
= θ = 45°
Q6 If sin6θ + cos6θ = 1/3, 0° ≤ θ ≤ 90°, then what is the value of sinθ.cosθ?
Solution: sin6θ + cos6θ = 1/3
= (sin²θ + cos²θ)³ = sin6θ + cos6θ + 3sinθ.cosθ (sin²θ + cos²θ)
= 1 = 1/3 + 3sin²θ.cos²θ
= sin²θ .cos²θ = 2/9
= sinθ.cosθ = √2/3
Q7 If (2cos A + 1) (2 cos A – 1) = 0, (0° ≤ A ≤ 90°) , then find the value of A?
Solution: (2cos A + 1) (2cos A – 1) = 0
= 4cos²A – 1 = 0
= 4cos²A = 1
= cos²A = 1/4
= cos A = 1/2
= A = 60°
Q8 If cos²θ – sin²θ = 1/2, (0 ≤ θ ≤ 90°), then find θ?
Solution: cos²θ – sin²θ = 1/2
= 2cos²θ – 1 = 1/2
= 2cos²θ = 1 + 1/2
= 2cos²θ = 3/2
= cos²θ = 3/4
= cosθ = √3/2
= θ = 30°
Q9 If tan x = cot (60° + 6x), then what is the value of X?
Solution: If A + B = 90°
= then, tan A = cot B
= tan x = cot (60° + 6x)
= 60° + 6x + x = 90°
= 60° + 7x = 90°
= 7x = 90° – 60° = 30°
= x = 30°/7
Q10 If 3(cosec²A + cot²A) = 5, then A is equal to:
Solution: 3(cosec²A + cot²A) = 5
= 3(1 + cot²A + cot²A) = 5
= 1 + 2cot²A = 5/3
= cot²A = 5/3 – 1 = 2/3
= cot²A = 2/6 = 1/3
= cotA = 1/√3
= A = 60°
Recommended Reading
Difference between Circle and Sphere (Key Differences)
Difference between Pyramid and Prism with Examples (Key Differences)
Area of Triangle Class 9- Definition, Important Formulas, Examples, Practice Questions & FAQs.
Basic Trigonometry Formulas for Beginners in 2024- Definition, Table, all Important Formulas & FAQs.
Frequently Asked Questions
Q1 What is Trigonometry?
Trigonometry is a branch of mathematics that deals with the relations of the sides and angles of the right angle triangle.
Q2 What are the three main functions in trigonometry?
The three main functions in trigonometry are sine, cosine and tangent.
Q3 Why trigonometry is important for SSC CGL exam?
Trigonometry is a fundamental part of mathematics and it is used in many different areas of the exam.
Q4 Who is the father of trigonometry?
Hipparchus is the father of trigonometry.
Q5 Is trigonometry important for SSC CGL?
Trigonometry is an important part of the SSC CGL exam and candidates who want to do well on the exam need to have a strong understanding of trigonometry.
Q6 Which subject is most important in SSC CGL?
All subjects are important for the SSC CGL exam but mathematics stands out as the most subject due to its scoring potential.
