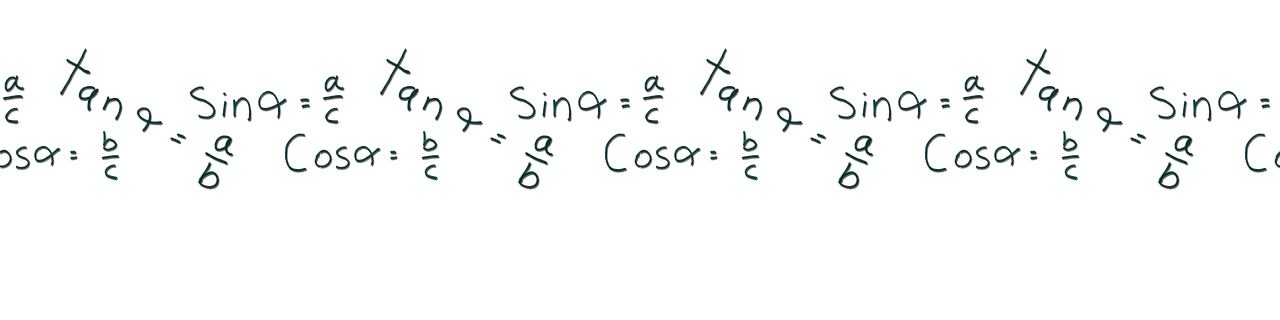In this article you will find Basic Trigonometry Formulas. Trigonometry is important in various fields such as engineering, physics, architecture, astronomy, and navigation. It helps in solving problems involving angles, distances, and periodic phenomena. Applications include calculating forces in structures, determining trajectories of objects, designing buildings, analyzing waves, and navigating ships and aircraft.
Table of Contents
What is Trigonometry?
Trigonometry is a branch of mathematics that deals with the relationships between the angles and sides of triangles. It encompasses concepts such as sine, cosine, tangent, and their reciprocal functions, as well as their inverses. The word “Trigonometry” is derived from two Greek words “trigonon,” meaning “triangle,” and “metron,” meaning “measure.” So, trigonometry literally means “measurement of triangles.”
What is Trigonometry Formulas?
Trigonometry formulas are mathematical expressions that describe relationships between angles and sides of triangles. These formulas are used to calculate unknown angles or side lengths in triangles, based on known information. They include relationships such as the Pythagorean identity, sine cosine, and tangent formulas, which are fundamental for solving trigonometric problems. Trigonometry formulas provide a systematic way to analyze and solve problems involving triangles and angular measurements.
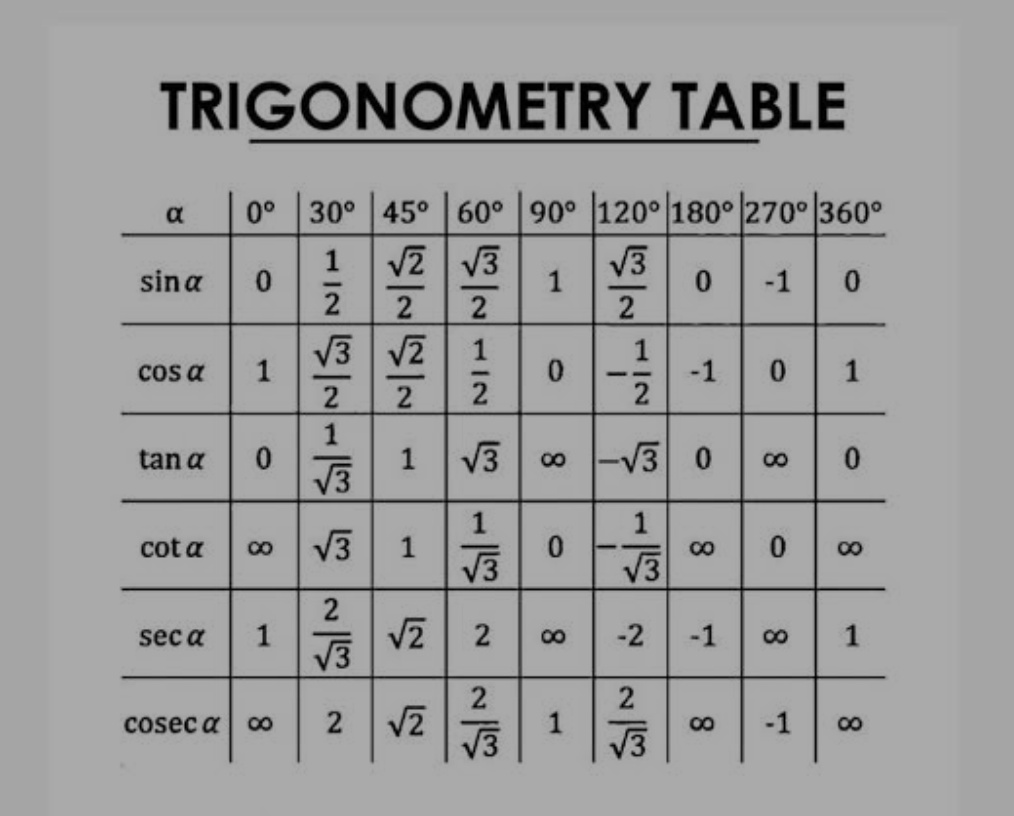
Trigonometry Table
Trigonometric table, also known as a trig table, is a table that lists the values of trigonometric functions (sine, cosine, tangent, etc.) for various angles. These tables are used to quickly find the values of trigonometric functions without the need for complex calculations, especially in the days before calculators were widely available. Each row typically represents a specific angle (measured in degrees or radians), and the columns correspond to different trigonometric functions and their values for that angle.
(Basic Trigonometry Formulas)-Trigonometric Ratios
Trigonometry ratios are mathematical relationships between the sides of a right triangle and its angles. The primary trigonometric ratios are:
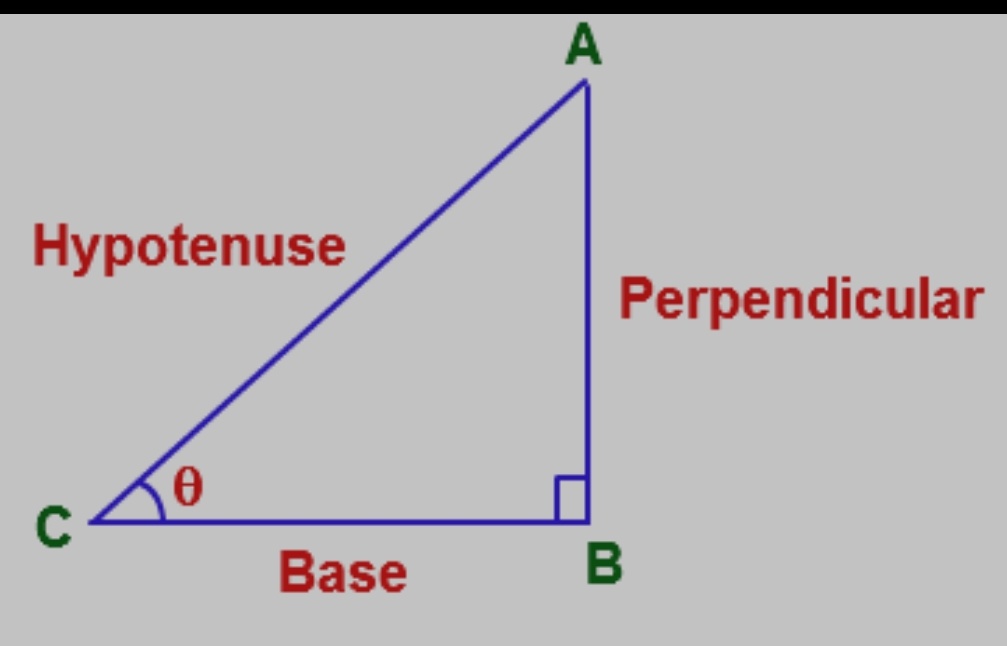
- Sin θ = Perpendicular/Hypotenuse
- Cos θ = Base/Hypotenuse
- Tan θ = Perpendicular/Base
- Cot θ= Base/Perpendicular
- Sec θ = Hypotenuse/Base
- Cosec θ = Hypotenuse/Perpendicular
(Basic Trigonometry Formulas)–Pythagorean Identities
The Pythagorean identity in trigonometry is a fundamental relationship between the sine and cosine functions of an angle in a right triangle. It states that the square of the sine of an angle plus the square of the cosine of the same angle is always equal to 1.These identities are used to convert one trigonometry ratio into other. The Pythagorean Trig identities are mentioned below:
- Sin2 θ+Cos2θ=1
- Sec2θ- Tan2 θ=1
- Cosec2θ-Cot2θ =1
(Basic Trigonometry Formulas)-Reciprocal Identities
The reciprocal trigonometric identities are a set of relationships between trigonometric functions that involve reciprocals of one another. These identities are derived from the definitions of the primary trigonometric functions and are helpful in simplifying expressions and solving equations.
- Sinθ=1/Cosecθ or Cosecθ=1/Sinθ
- Cosθ=1/Secθ or Secθ=1/Cosθ
- Tanθ=1/Cotθ or Cotθ=1/Tanθ
(Basic Trigonometry Formulas)- Even-Odd identities
In trigonometry, even and odd identities refer to properties of trigonometric functions with respect to symmetry.
- Sin(-x)=-Sin (x)
- Cos(-x)=-Cos (x)
- Tan(-x)=-Tan (x)
(Basic Trigonometry Formulas)-Periodicity Identities
In trigonometry, the periodicity identity refers to the property that trigonometric functions repeat their values at regular intervals. These can be expressed as:
- Sin(x+2π) = Sin (x)
- Cos(x+2π) = Cos (x)
- Tan(x+π) = Tan (x)
(Basic Trigonometry Formulas)- Co-function Identities
The co-function identity in trigonometry states that the sine of an angle is equal to the cosine of its complementary angle, and vice versa. Mathematically, it can be expressed as:
- Sin (90° -x) = Cos x
- Cos (90° – x) = Sin x
- Tan (90° – x) = Cot x
- Cot (90° – x) = Tan x
- Sec (90° – x) = Cosec x
- Cosec (90° – x) = Sec x
(Basic Trigonometry Formulas)-Product-to-Sum Formulas
- Sin(A)Sin(B)=½ [Cos(A-B)-Cos(A+B)]
- Cos(A)Cos(B)= ½[Cos(A-B)+Cos(A+B)]
- Sin(A)Cos(B)=½[Sin(A-B) + Sin(A+B)]
(Basic Trigonometry Formulas)– Sum-to-Product Formulas
- Sin(A) + Sin (B) = 2Sin[(A+B)/2] Cos[(A-B)/2]
- Sin(A) – Sin(B) = 2Sin[(A-B)/2]Cos[(A+B)/2]
- Cos(A)+Cos(B) =2Cos[(A+B)/2]Cos[(A-B)/2]
- Cos(A)-Cos(B) = 2Sin [(A+B)/2]Sin[(B-A)/2]
Recommended Reading:
Difference between Pyramid and Prism with Examples (Key Differences)
Area of Triangle Class 9- Definition, Important Formulas, Examples, Practice Questions & FAQs.
Frequently Asked Questions:
1)What are the basic trigonometric ratios?
Answer – Sine, Cosine, Tangent, Cotangent, Secant, and Cosecant.
2) What are the 3 main functions of trigonometry?
Answer – Sin, Cos, Tan are 3 main functions in trigonometry.
3) Trigonometry formulas are applicable to which triangle?
Answer – Right-angled triangle.
4) What is Trigonometry?
Answer – Trigonometry is the Branch of mathematics dealing with the relations of the sides and angles of triangles and with the relevant functions of any angles.